Turning Data into Direction: The Power of Bayesian Search Theory
Navigating Uncertainty with Bayesian Probability
One of the most captivating news stories every now and then is when a plane goes missing over the ocean. Millions of people start imagining and hypothesising the possibilities as to what happened to it. Countless tips and suggestions flood the information space, leaving officials hard-pressed to conduct the search effectively amidst the conflicting demands of families.
Vast stretches of sea and land are potential search areas. Where should one even begin? How do we allocate limited resources – planes, satellites, search crews – to maximise the chances of successfully finding the plane?
One of the better-known examples is the search for Malaysia Airlines Flight MH370 in 2014, which vanished between Malaysia and Vietnam, with a glimpse of radar later showing it over the Andaman Sea. It puzzled the world. With only scattered radar data, search teams had to decide where to focus their efforts over millions of square miles of ocean. The search wasn’t random or based purely on instinct. Behind it was a method known as Bayesian Search Theory (BST). Even if the wreckage in this specific example remains elusive in the unfathomably vast Indian Ocean, the concept has proven its usefulness for example in locating the lost submarine USS Scorpion during the cold war.
I am a big fan of the Bayesian conception of probability. At its core, Bayesian probability is a way of thinking about uncertainty and updating our beliefs in light of new evidence. Unlike traditional (or "frequentist") probability, which often treats probability as a long-run frequency (like flipping a coin or rolling dice enough times), Bayesian probability is about degrees of belief – how strongly we believe something is true, and how that belief changes as we gather more information.
Think of it this way: You're trying to figure out whether it will rain in the evening. You start with a belief based on a weather forecast that predicts a 60% chance of rain. That 60% isn't a fact about the future, it's a reflection of your uncertainty about it. You don’t know for sure, but you’re leaning toward thinking it might rain because of prior estimate.
Now as the day goes on, you observe dark clouds gathering, which makes you more confident in the forecast. At that moment, you start thinking even more strongly that it is going to rain – and revise your belief upward. Now you think there’s, say, an 80% chance of rain. The key here is that your belief changed when you saw new evidence (the dark clouds), and Bayesian probability is precisely about this process of updating your beliefs as new information becomes available. That’s more or less what is happening in your brains naturally, Bayesian probability offers a coherent and systematic mathematical framework for this process.
Bayesian Search Theory merges the above-described conception of the Bayesian probability with the art of search. It doesn’t just give you a place to look, it helps you think systematically about where to focus your efforts based on available information.
When something goes missing, whether it’s a plane above the ocean, a person in the wilderness, or even a set of car keys, there’s a frustrating mix of too much space and too little information. You have some clues: maybe the plane’s last known location or the range of the car keys’ Bluetooth signal. But beyond that, it's all guesswork.
Traditional search methods – searching from point A to point B systematically – can be inefficient when dealing with large, uncertain areas. Like combing through an area of ocean the size of Australia to find a plane-wreck. It’s like finding a needle in a haystack, but exponentially harder. It would take literal years, if not decades.
For a practical illustration, imagine you've dropped your keys into a nearby small lake while rowing. It could happen to anyone! To find them, BST starts with the simple acknowledgment that you don’t know where the target is, but you have some ideas. Some theories, hypotheses. You may know where the missing plane was last seen or at what time do you last remember having the keys. This is your prior information – your best guess based on what earlier evidence suggested.
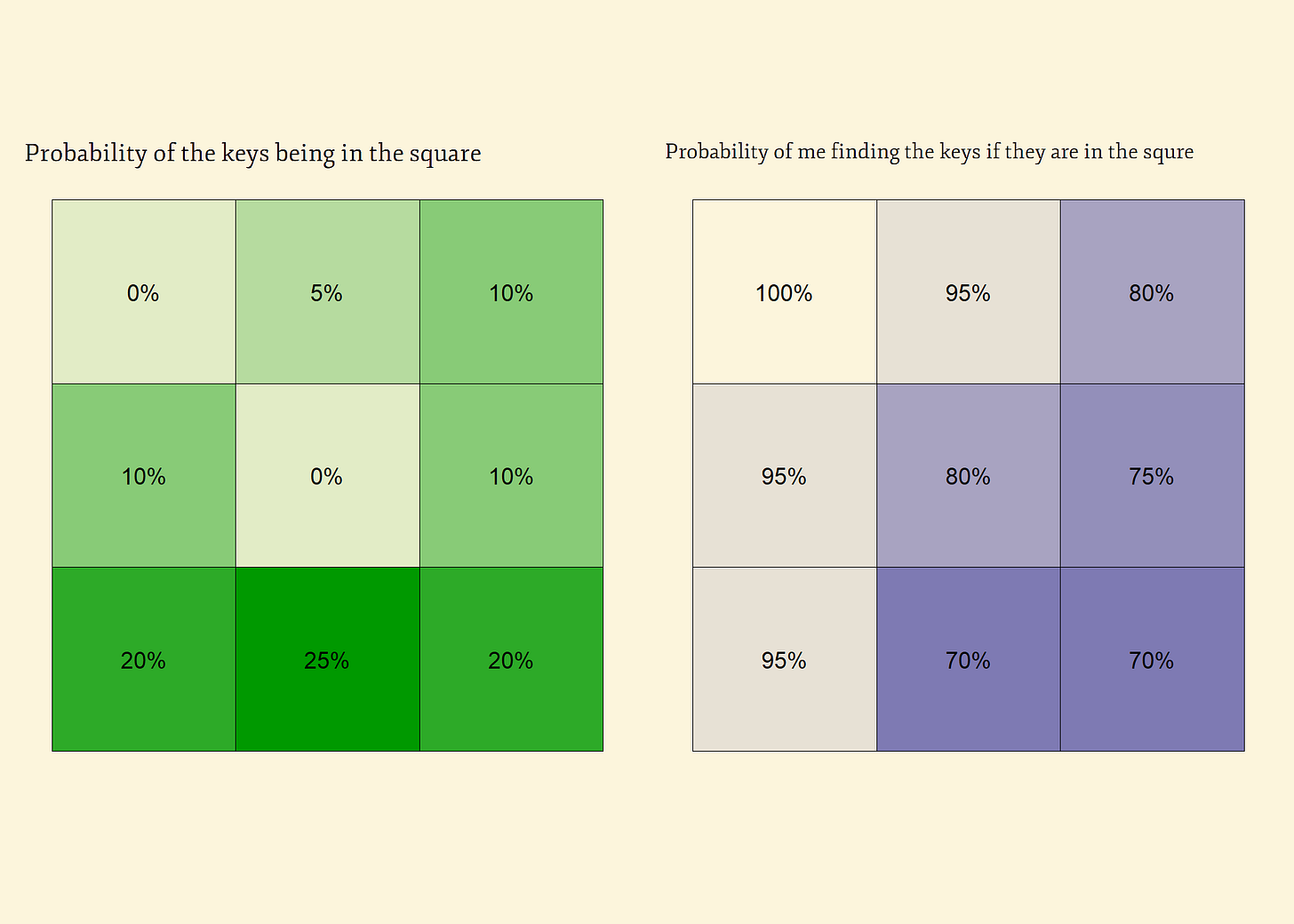
Let us divide our hypothetical lake into a 3x3 grid for simplicity, where I have assigned probabilities on how confident I am that the keys are in that portion of the lake.
I started from the top left where I clearly remember having the keys with me, so finding them right at the start is impossible. I progressed with my rowing lap counter-clockwise around the lake. That means the keys are not at the centre of the lake either, and I am quite sure (but not certain) that I noticed them having been lost by some point at the end of the lap. My best guess is that they are somewhere in the bottom portion of the grid.
The lake, however, does not have uniform depth. At some squares of the pond-grid I have 100% chance of finding the keys by searching in the square if they actually are there. In others, the water is so deep the probability decreases to 70%. Coincidentally, the area where I most likely dropped the keys is also the deepest and most difficult to search.
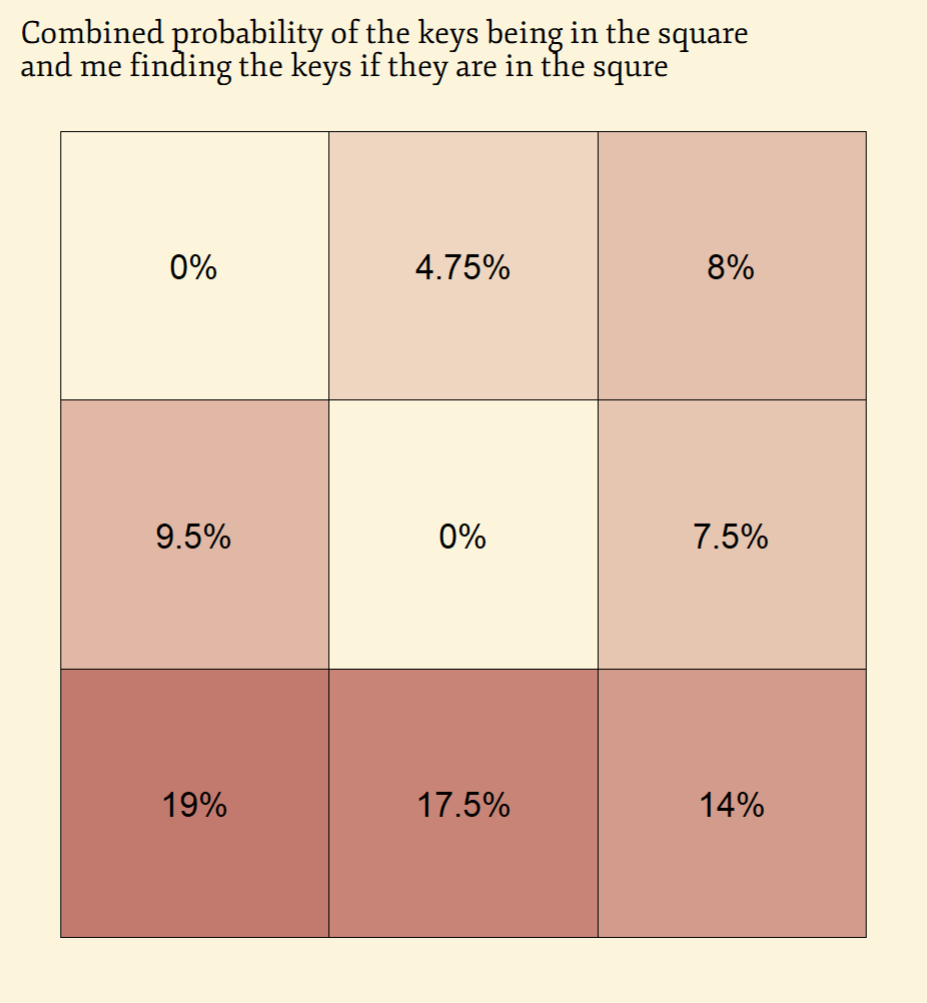
Naturally, these factors should be combined. It is not the most cost-efficient thing to search the deepest portions, even if the chance for the keys to be there is a bit larger than elsewhere.
Thus, the most cost-efficient approach is to start not where the keys are most likely to be, but where the conditional probability of finding them, given they are there, is highest. But that’s not the end of it. Once you begin searching, new information (or lack thereof) starts to emerge, and this is where Bayesian updating comes into play.
At the heart of Bayesian updating is Bayes’ Theorem, a simple mathematical formula that guides how we update our beliefs. While we don’t need to dive too deep into the maths, understanding the core idea will help us see why this is such a powerful tool.
Bayes’ Theorem tells us that
The formula looks fancy, but it boils down to something very simple:
A = Prior belief: What you initially think is true. For example, “my keys are in this grid square with the probability of 20%”
B = New evidence: Information that comes in and gives you reason to adjust your thinking. In our example, you might search the bottom left square of the 3x3 grid.
P(A|B) = Updated belief (posterior): Your new, more refined belief after considering the evidence. For example your new probabilities to find the keys from the squares of the grid, given whether you found the keys in the square.
The updated belief can be re-articulated as the product of the prior belief and your new evidence given the hypothesis being correct. Divided by the probability of the evidence being true.
So, Bayesian updating is the process of taking what you know, factoring in the new evidence, and coming up with an updated, more accurate belief. It’s a dynamic process, where each new piece of information nudges your thinking in a better direction.
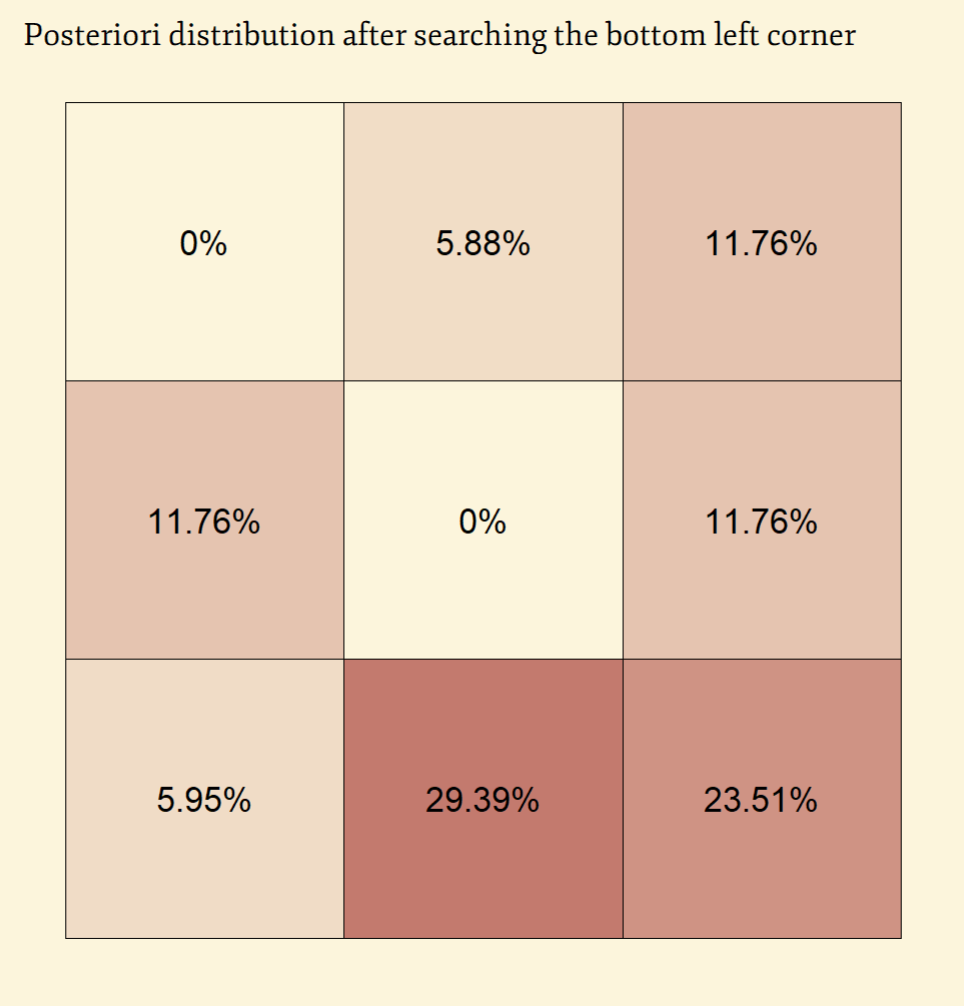
Should you start the search for the lost keys from the square with the biggest probability (bottom left) and fail to find them there, you would calculate the posterior probability for the square in question after searching it as
And plugging the numbers we have
for the posterior probability in bottom left square that was just searched1. Subsequently after the first search we will normalise the probabilities and they become our new priors for the next step.
Notice that the probability for our bottom left square was not reduced to zero, as there remained a chance that the keys really were present in the square, we just did not find them. And onwards we would progress to the next square that holds the biggest probability to have the keys. And then the next one, and so on. All until the end when our allocated resources (time, money) have been exhausted, the relative cost-benefit calculation becomes too costly or we simply find what we were looking for.
Bayesian Search Theory ensures the efficient allocation of limited resources when searching a target. The overarching concept of Bayesian probability, however, is a valuable tool in countless fields. Be it a lost shipwreck, looking for a bird’s nest in context of wildlife conservation, medical diagnosis, economic, political or sports forecasting or just keys like in our example, you are bound to get the best bang for the buck. Most fields require a parsimonious framework to systematically update your beliefs in face of new information. Bayes provided it. You should use it.
The P(not found anywhere) in nominator is calculated as summing up P(keys are in the square) x P(keys not found in the square) of every square.


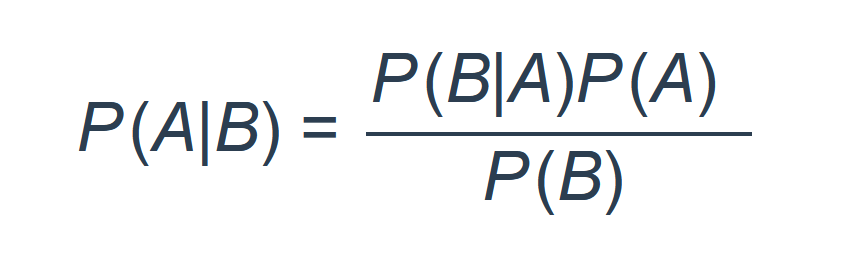

Great post, Julius! This was such a helpful illustration of Bayesian theory, and I suspect I'll come back to this piece every so often. :)